
[python]백준_1256 : 사전
[python]백준_1256 : 사전
📋 [ python ] 시리즈 몰아보기 (3)

🚗현대인을 위한 3줄요약.
같은 자료를 반복해서 참고해야 한다면 dp(dynamic programming)를 이용해 시간복잡도를 줄일 수 있다.
📌전체코드
우선 전체 코드는 다음과 같다.
| 1 | import sys |
| 2 | input = sys.stdin.readline |
| 3 | |
| 4 | n, m, k = map(int, input().split()) |
| 5 | dp = [[1]*(m+1) for _ in range(n+1)] |
| 6 | |
| 7 | for i in range(1, n+1): |
| 8 | for j in range(1, m+1): |
| 9 | dp[i][j] = dp[i-1][j] + dp[i][j-1] |
| 10 | |
| 11 | if dp[n][m] < k: |
| 12 | print("-1") |
| 13 | else: |
| 14 | res = "" |
| 15 | while True: |
| 16 | if n == 0 or m == 0: |
| 17 | res += "a" * n |
| 18 | res += "z" * m |
| 19 | break |
| 20 | flag = dp[n-1][m] |
| 21 | if flag >= k: |
| 22 | res += "a" |
| 23 | n -= 1 |
| 24 | else: |
| 25 | res += "z" |
| 26 | m -= 1 |
| 27 | k -= flag |
| 28 | print(res) |
해당 코드에서 면밀히 살펴볼 부분은 다음과 같다.
dp[]: dp 진행을 위해 사용하는 배열. dp에 저장한 값을 참고하는 것으로 코드가 진행된다.문제해결: 해당 문제는 알고리즘을 제쳐두고라도 문제해결법이 꽤나 어렵다.
각 키워드가 포함된 문단별로 나눠서 분석해보자
👉dp[]
dp(dynamic programming)은 동적 계획법이라고도 하며 하나의 큰 문제를 여러 개의 작은 문제로 나누어서 그 결과를 저장하여 다시 큰 문제를 해결할 참고하는 일종의 방법론이다. 재귀법과 유사한듯 보이지만 이미 구한 값에 대해서는 계산을 하지 않는다는 점에서 시간복잡도의 차이가 있다.
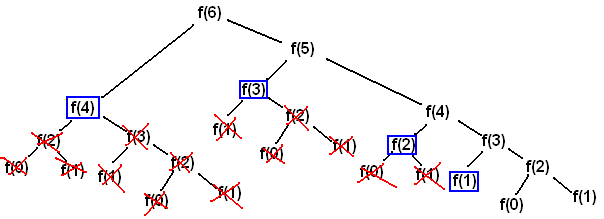
위 사진은 dp를 언급할 때 가장 자주 사용되는 예시인 피보나치 수열의 흐름도이다. 일반적인 재귀법을 채택했을 때 6번째 피보나치 수( = f(6) )를 구하기 위해선 다음과 같이 수많은 계산을 필요로 한다.
이때 dp를 활용하면 중복되는 결과값( = 붉은색 X표시 부분)은 더이상 계산하지 않고 특정 영역에 저장된 값을 불러오는 것으로 해결할 수 있다. 즉 큰 문제인 f(4)를 구하기 위해 작은 문제인 f(1) ~ f(2)는 계산을 생략하고 또다른 작은 문제인 f(3)만 계산하면 된다.
이를 해당 문제에 적용해보자. 문제에서 a와 z로 이루어진 사전을 작성하는것이 핵심이다.
| 1 | dp = [[1]*(m+1) for _ in range(n+1)] |
| 2 |
a가 n개, z가 m개라고 가정했을 때 n과 m의 조합은 중복 순열의 경우의 수를 가지게 된다. 즉 중복되는 계산값이 존재하고 n과 m의 조합만큼의 경우의 수를 가지게 되므로 dp가 사용될 수 있다.
👉문제해결
중복순열의 경우의 수를 구하기 위해선 팩토리얼(factorial)의 계산이 요구되는데 이를 dp를 활용해 구해보도록 하자. 우선 점화식을 위해 예제를 활용해보자.
a = 2, z = 2일때의 경우를 가정했을 때 결과값은 다음과 같다.
- aazz
- azaz
- azza
- zaaz
- zaza
- zzaa
이중 절반은 a로 시작하고 나머지 절반은 z로 시작하며 모든 경우의 수는 a 또는 z로 끝나게 된다. 만약 k가 2라면 a부터 시작, 4라면 z부터 시작하게 된다. 기준을 a로 시작하는가로 잡았을 때 다음과 같은 점화식이 성립된다.
- F(N,M) : N개의
a와 M개의z로 만들 수 있는 경우의 수 - F(N,M) = F(N-1, M) + F(N, M+1)
- dp[n][m] = dp[n-1][m] + dp[n][m-1]
즉 a를 기준으로 했을 때 dp[n-1][m]이 되겠다. 즉 k가 해당 식의 값보다 작거나 같으면 a로 시작, 그렇지 않으면 z로 시작하게 된다.
| 1 | for i in range(1, n+1): |
| 2 | for j in range(1, m+1): |
| 3 | dp[i][j] = dp[i-1][j] + dp[i][j-1] |
이때 k번째 수 또한 사전순으로 k번째 수이므로 k가 z로 시작하면 k = k - flag를 해줘야 한다. 예를들어 n = 2, m = 2, k = 5일때, k는 3보다 크므로 k는 z로 시작하나 z로 시작하는것 중 5번째가 없으므로 z로 시작하면 앞의 a로 시작하는 경우의 수는 빼줘야 한다는 뜻이다.
| 1 | if dp[n][m] < k: |
| 2 | print("-1") |
| 3 | else: |
| 4 | res = "" |
| 5 | while True: |
| 6 | if n == 0 or m == 0: |
| 7 | res += "a" * n |
| 8 | res += "z" * m |
| 9 | break |
| 10 | flag = dp[n-1][m] |
| 11 | if flag >= k: |
| 12 | res += "a" |
| 13 | n -= 1 |
| 14 | else: |
| 15 | res += "z" |
| 16 | m -= 1 |
| 17 | k -= flag |
| 18 | print(res) |
단어를 생성하기 위한 변수 res를 빈 문자로 초기화 하고 위의 점화식을 참고해 식을 작성한다. flag를 a로 시작했을 경우로 지정해준 후 flag와 k의 값을 비교해가며 식을 진행, n 혹은 m이 0인 경우(계산이 끝났을 경우) res에 남은 문자를 더해주고 break를 진행한다.
참고문서
👨💻 관련 포스트

[python] snscrape를 이용한 웹크롤링 및 데이터 시각화
[python] snscrape를 이용한 웹크롤링 및 데이터 시각화
python 모듈인 snscrape, wordCloud 모듈을 이용해 twitter에서 특정 키워드가 포함된 트윗을 크롤링하여 언급 빈도수에 따라 시각화된 자료를 생성할 수 있다.
2023-03-21

[python]백준_1456 : 거의 소수
[python]백준_1456 : 거의 소수
[python] 백준 1456 : 거의 소수. 해당 문제는 에라토스테네스의 채를 이용해 소수를 판별, 시간복잡도를 줄여 문제를 해결할 수 있다.
2023-04-11
💡 로그인 하지 않아도 댓글을 등록할 수 있습니다!